Answer to Question #13095 Submitted to "Ask the Experts"

Is it possible to calibrate a Ludlum 44-9 pancake probe to a plated source of depleted uranium of known activity? Do you have any idea what the counting efficiency might be counts per second per disintegrations per second (cps dps^-1). And then might that be converted to a dose rate in microGray per hour (µGy hr^-1), knowing the energy of the radiations entering the GM tube?

The short answer is yes, it is possible to calibrate the Ludlum probe to a plated source of depleted uranium. The longer answer requires some additional information about what quantity you wish to evaluate and under what irradiation conditions. I'll try to provide some guidance.

Depleted uranium sources are often used as beta radiation calibration sources, and I shall assume here that that is your major interest. Most commonly, the sources are depleted uranium slabs of thicknesses greater than the beta particle ranges and with facial areas greater than the active facial area of the detector. The sources are typically covered with a tissue equivalent thickness of plastic equal to the nominal dead skin thickness of 7 mg cm^-2, which acts as an effective alpha radiation shield as well as providing a measure of dose rate to the live skin (some attenuation may also occur in the detector window). The expected soft tissue live skin dose rate at the surface of such a source is about 2.30 mGy h^-1 mostly associated with beta radiation from ^234mPa, which has a maximum beta energy of about 2.27 MeV.

Unfortunately, this same dose rate value would not likely apply to a plated surface source. Even if you cover it with the 7 mg cm^-2 tissue equivalent layer to attenuate the alpha radiation, the beta/electron distribution from the surface source would not be the same as from the infinitely thick source. The manufacturer of the probe does provide some efficiencies for limited beta sources. These efficiencies are usually quoted for surface sources in which the activity is spread over an area less than or possibly equal to the active facial area of the probe. For the Ludlum 44-9 probe that you cite, the manufacturer shows beta efficiencies for the radionuclides ¹⁴C (Eff = 0.05; E_max = 0.156 MeV), ⁹⁹Tc (Eff = 0.19; E_max = .29 MeV), and ³²P (Eff = 0.32; E_max = 1.7 MeV). The manufacturer also provides efficiency for ⁹⁰Sr-⁹⁰Y, the shown efficiency being 0.22; the problem with this value is that it is the result of two different beta distributions, the ⁹⁰Sr being characterized by a maximum beta energy of 0.53 MeV while the ⁹⁰Y has a maximum beta energy of 2.28 MeV; the given efficiency value of 0.22 seems inconsistent with expectations based on the other given efficiencies.

I would judge that the Ludlum 44-9 detection efficiency for the relatively high energy (E_max = 2.27 MeV) beta radiation from a small area surface source of ²³⁸U (^234mPa) should be in the range from 0.35 to 0.40 cts beta^-1 (the beta yield for the protactinium radiation is 0.982). If your plated source is smaller in area than the 15.5 cm² active area of the probe, I would think this estimated efficiency would be reasonable. The source should be covered with about a 7 mg cm^-2 tissue-equivalent thickness of material to eliminate the response to alpha radiation. We should also note that the thin window of the probe is recessed approximately 3 mm within the casing of the probe head, and it is typically covered with a protective screen that blocks about 21% of the window area. Based on the manufacturer's quoted efficiencies, I would estimate that the probe casing was likely held in near contact with the source surface when the efficiencies were determined.

If you have access to any version of the Varskin code, this would allow the easiest estimation of the dose rate for whatever the exposure conditions might be. The code allows for calculations of dose to live skin with allowances for variations in source characteristics and the presence of an airspace and/or other intervening materials between the source and the receptor. If you do not have access to the code, it may still be possible to make an estimate of expected tissue dose rate at the location where the measurement is made. I will attempt to demonstrate this with a simple case in which the source dimensions are considerably smaller than the active window area of the detector and when the source is centered at a close distance from the potential tissue receptor. I shall not attempt to correct for attenuation in air or any other materials that may be present (e.g., dead skin layer, clothing).

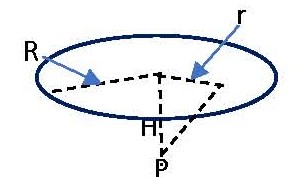
In the sketch the disc area represents the area of tissue over which we wish to average the dose rate. For skin dose calculations the area often used is 10 cm². If we simply want the maximum dose rate at a point on the skin surface, we simply need to calculate the beta fluence rate at the distance of interest (H) at a point directly above the source, P. In such an instance the unattenuated beta fluence rate. Φ, from an isotropic radionuclide source emitting S beta particles per second would be given by

Φ = S/4πH²    (1).

If we wish to average the fluence rate and dose rate over a disc-shaped area of radius R as shown in the figure, we would solve the following differential equation:

dΦ = S [2πrdr/4π(H² + r²)]/πR².

This can be integrated between the limits r = 0 to r = R to obtain

Φ = (S/4πR²) ln[(H² + R²)/H²]   (2).

As an example, if the uranium source emitted 20 beta particles per second from ^234mPa, and we desired the dose rate to a point 0.5 cm from the source, we would calculate the fluence rate from equation 1 as

Φ = 20 s^-1/4π(0.5 cm)² = 6.37 cm^-2 s^-1.

The dose rate is given by the product of the fluence rate and the average mass collision stopping power for the beta distribution. As an estimate, we shall use the value of the collision stopping power at the average beta energy, which for ^234mPa is 0.825 MeV; the stopping power value, available at this NIST web page, is 1.87 MeV cm² g^-1.The estimated dose rate, D, in µGy h^-1 is then

D = (6.37 cm^-2 s^-1)(1.87 MeV cm² g^-1)(1.6x10^-6 ergs Mev^-1)(10 g-mGy/100 ergs)(10³ µGy/mGy)(3600 s h^-1) = 6.9 µGy h^-1.

If we rather wanted the dose rate averaged over a 10 cm² soft tissue area (radius of 1.784 cm) at the same 0.5 cm distance, equation 2 would yield

Φ = (20/4(10 cm²)) ln[(0.5² + 1.784²)/0.5²] = 1.31 cm^-2 s^-1.

Converting from fluence rate to the dose rate in the same manner as above we would obtain

D = 1.4 µGy h^-1.

Keep in mind that the above calculations are estimations, not accounting for any beta particle attenuation, and using a stopping power based on the average energy which would be somewhat different from the average stopping power based on the entire beta particle energy distribution. Also, the calculations were done for a point source, which might also be a reasonable approximation for a surface source with dimensions considerably smaller than the detector facial area. For a larger area source, however, the more correct solution would require integrating contributions from the entire source area. We shall not pursue that at this time. If you require such you could submit another question with more details about the source configuration, and we could follow up. I hope this has been helpful.

George Chabot, PhD, CHP