Answer to Question #12704 Submitted to "Ask the Experts"

I was doing an experiment with a ¹³⁷Cs gamma source of 0.74 MBq. The detector is an end window GM Tube–ZP1431 (Centronics) with useful window diameter of 27.8 mm and window thickness of 2–3 mg cm^-2. The source disc type is an evaporated and ultrasonically sealed gamma source at the center of a 25 mm diameter x 5 mm thick plastic disc and covered with 1 mm thick plastic lid with active diameter of source as 6 mm. The distance between source and detector is maintained fixed at 2 cm. Since the distance between source and detector is 2 cm, I'm interested in knowing the average exposure rate(E) over the window of the detector. To calculate this, I used the formula:

E = (AG/r²) ln(d²+r²)/d²

Where,

A = activity of source (0.74 MBq in my case),

G = gamma ray air kerma dose rate constant (0.73 mGy h^-1 MBq^-1 at one centimeter),

r = radius of detector (1.39 cm),

D = distance between source and detector (2 cm).  

Is my approach to calculate the dose/exposure seen by the detector, considering the distance between source and detector to be as small as 2 cm, correct using this formula? Also, is the value of G = 0.73 mGy MBq^-1 valid for this small distance of 2 cm?

If not, what is the correct approach to calculate the value of activity/dose seen by the detector when placed at 2 cm away from source. My experimental setup is such that I can't change the distance between source and detector beyond 2cm. If you need any further details to answer my questions, please let me know.

I believe your basic concern about whether the gamma ray air kerma rate constant can be applied in this situation arises from the fact that the detector dimensions are significant compared to the perpendicular distance from the source to the surface. As a result, pathlengths from the source to different parts of the detector are variable. In such an instance, the gamma ray constant may be used at a given distance, but the ultimate calculation must be done by determining the average value of the dose rate or exposure rate throughout the detector volume. The equation that you used is proper to evaluate the average exposure rate over the surface of the window, but this will not be the same as the average exposure rate throughout the volume of the detector.

The active source diameter of 6 mm that you cite is sufficiently small that it will not have a very notable effect on the calculations that we are doing here, although it does add a small amount of uncertainty to the results that are based on assumption of a point isotropic source. Based on your description of the source, I assume that the plastic covering is sufficient to stop all beta radiation from the source. We have not attempted to include effects of gamma attenuation in the plastic source holder; such might account for a decrease of two or three percent in the results compared to what we obtain below.

After checking on the specifications for your detector, I see that the detector has an apparent depth of about 4.0 cm (you should confirm whether this is the effective depth of the detector) and your cited radius of 1.39 cm. The proper calculation is typically done by calculating the mean value of the exposure rate throughout the volume of the detector using a standard integral calculus approach. For a point isotropic source with activity A and gamma ray air kerma rate constant Γ; a cylindrical shaped detector with a radius of R and a depth of H; the source centered below the detector face with a perpendicular distance D from the source to the center of the detector face, and assuming no significant attenuation of gamma radiation in the source covering, air, or in the detector window or gas, the average exposure rate through the detector volume would be given by

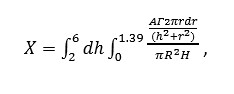
where h represents the perpendicular distance from the source to any depth in the detector, and r is the radial distance from the central detector longitudinal axis to a receptor point at that depth in the detector volume, as shown in the sketch below.

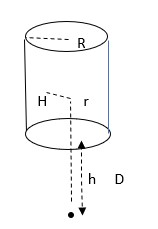
The limits on h go from 2 cm, the distance from the source to detector window, to 6 cm, the distance from source to the back flat side of the detector. The volume of the detector, πR²H, in the denominator of the above integral expression is the mathematical result of the integration from r = 0 to R and from h = D to D+H of the differential volume element 2πrdrdh.

The above integral was evaluated numerically with A = 0.74 MBq, T = 0.73 mGy h^-1 MBq^-1 at one centimeter, and integration limits as shown in the above equation. The result obtained was 0.041 mGy h^-1. If one had simply calculated the air kerma rate at a fixed distance of 2 cm from the source, the result would have been 0.135 R h^-1, about 3.3 times greater than the value averaged throughout the detector volume. The equation that you used for the average exposure rate over the window surface would have yielded 0.110 mGy h^-1, about 2.7 times the volume-averaged result. We might further note that at times investigators make approximations to expected detector responses by simply doing a point-to-point calculation using the distance from the source to the center of the detector volume to provide some compensation for the effect of increased distance to parts of the detector volume. If we had done so in this case, the distance would have been 4 cm, and the result would have been 0.034 mGy h^-1, about 83% of the average value that we calculated.

I hope the above is instructive and helpful for you.

George Chabot, PhD, CHP